又到了一年一度研究生要畢業的季節,開始要完成實驗
通常實驗都需要蒐集很多樣本作統計,來判斷所提出的方法可不可靠
但是需要蒐集多少樣本呢?
學過機率與統計的都知道
依據中央極限定理和大數法則,
想要做一份具有相當準確性的統計,是不需要蒐集所有母體樣本的
只要蒐集到一定程度,其統計結果就能代表母體全部
但到底要蒐集到什麼程度呢?
有沒有一個明確的準則?
在此介紹一個Dillman於2000提出的公式
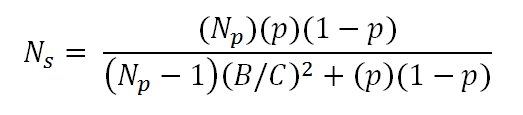
Ns = 須完成的樣本數
Np = 母群體規模
(p)(1-p):母群體異質性程度,通常設p=0.5 (此為最保守策略,因為變異數最大的情況會發生在母體兩半互為不同類別)
B:可容忍的抽樣誤差,通常設0.03 (抽樣誤差正負3%)
C:可接受的信賴區間(信心水準),通常設1.96 (該數值為可接受的信賴區間95%所對應的Z分數)
這個式子,其意義在於設定一個信心水準和可接受的抽樣誤差範圍,來降低所需要的樣本數。
範例
將母群體規模為600及100000,使用以上的數值
代入此式
當母體規模為600,所需樣本數:384。
當母體規模為100000,所需樣本數:1056。
全站熱搜


 留言列表
留言列表