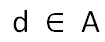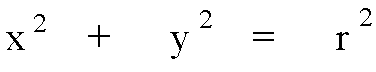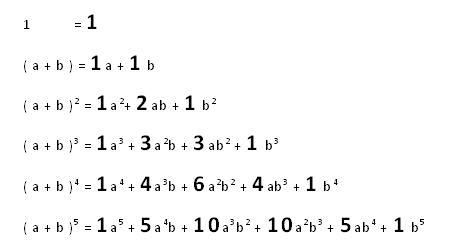Frank's 資訊科技潮流站

動態規劃
1. 大問題可以分解為子問題
2. 每一個子問題的答案可以被儲存起來 供下次直接取用 不必再重新計算
 

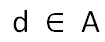
Let A sequence of number be
A1,A2,…..,Ai,…..,An in an increasing order  
N is the number of elements

Multiple Loop To Recurrence Function

---

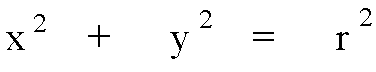
割圓術到底能不能算出無限位數的 pi π呢......?
首先呢，我們要先知道圓形的一個公式
Here's the formula of a round.
其中，  r   是半徑
r is the radius of the round.
運用這個公式，我們可以求得在一個圓形上出現的所有座標
Using this formula, we can get all the positions of the round.
但是可想而知，如果圓上面，每個座標都要求到...
其實是有無限多個！
所以，我們就把顯示座標限制在 
     _____   _____
( √整數 , √整數   )
However, the number of the positions on the round...is infinite..
So, we just show the positions that are square roots of integers.
     _____      _____
( √Integer, √Integer  )

可以一次計算多個數值的最大公因數 最小公倍數
[ 按此下載 ]
[ English Version is Available ]
程式碼 (僅供學習參考用) ：
#include<stdio.h>
#include<stdlib.h>
int lcm(int a,int b);
int gcd(int c,int d,int e);
int main(void)
{
   
    int g=1,get[10],c,re,re2,re3,gcd2,k;
       
    printf(" 《最大公因數、最小公倍數 計算機》 \n");
while(g=g)
{
      
    while(g==g)
    {
      printf("\n請輸入第 %d 個數值 ，輸入 0 開始計算： ",g);
      scanf("%d",&get[g]);
     
      gcd2=get[g-1];
     
      if(get[g]==0)
        break;
     
      g++;
    }
   
    g--;
   
    for(k=1;k<=g;k++) /* 排序，從小的數值排到大的 */
    {
      for(int i=1;i<=g;i++)               
      {
        if(get[k]>get[i])
          c=get[k],get[k]=get[i],get[i]=c;
      }
    }    
   
    re=re2=get[g];
             
    while(g>=2)
    {
     re3=re2;
    
     re=lcm(re,get[g-1]);
    
     re2=lcm(get[g],get[g-1]);  /* 計算 這次 最小公倍數 */
     re2 = gcd(get[g],get[g-1],re2); 
     gcd2 = lcm(re2,re3); /* 計算 這次 和 上次 最小公倍數 的 最大公因數 */
     gcd2 = gcd(re3,re2,gcd2); /* 計算 這次 和 上次 最小公倍數 的 最小公倍數 */
    
     g--;
        
    }
     printf("\n最大公因數 ： %d\n\n最小公倍數 ： %d\n\n=====================================",re,gcd2);
    
   g=1;
  
   printf("\n\n請輸入第 %d 個數值 ，輸入 0 離開程式： ",g);
      scanf("%d",&get[g]),g++;
     
      if(get[1]==0)
      {
        printf("\n");          
        break;
      }
}
}
   
   
int lcm(int a,int b)
{
    int c=b;
   
    if(a<b)
    c=a,a=b,b=c; /* a b 互換 */
   
    b=a-b;
   
    if(b!=0)
    {   
     while(a%b!=0)
     {
      c=b;
      b=a%b;
      a=c;
     }
    }
    else
    b=c;
   
    return b;
   
}
int gcd(int c,int d,int e)
{
    e = c * d / e;
         
    return e;
   
}
Code ( for reference only ):
#include<stdio.h>
#include<stdlib.h>
int lcm(int a,int b);
int gcd(int c,int d,int e);
int main(void)
{
   
    int g=1,get[10],c,re,re2,re3,gcd2,k;
       
    printf(" < LCM & GCD CALCULATOR > \n");
while(g=g)
{
      
    while(g==g)
    {
      printf("\nEnter #%d Value , Enter 0 to begin calculate : ",g);
      scanf("%d",&get[g]);
     
      gcd2=get[g-1];
     
      if(get[g]==0)
        break;
     
      g++;
    }
   
    g--;
   
    for(k=1;k<=g;k++) /* Sort, from small to big */
    {
      for(int i=1;i<=g;i++)               
      {
        if(get[k]>get[i])
          c=get[k],get[k]=get[i],get[i]=c;
      }
    }    
   
    re=re2=get[g];
             
    while(g>=2)
    {
     re3=re2;
    
     re=lcm(re,get[g-1]);
    
     re2=lcm(get[g],get[g-1]);  /* Calculate the lcm this round */
     re2 = gcd(get[g],get[g-1],re2); 
     gcd2 = lcm(re2,re3); /* Calculate the lcm of the gcd of this round and last round */
     gcd2 = gcd(re3,re2,gcd2); /* Calculate the gcd of the gcd of this round and last round */
    
     g--;
        
    }
     printf("\nL C M ： %d\n\nG C D ： %d\n\n=====================================",re,gcd2);
    
   g=1;
  
   printf("\n\nEnter #%d Value , Enter 0 to exit : ",g);
      scanf("%d",&get[g]),g++;
     
      if(get[1]==0)
      {
        printf("\n");          
        break;
      }
}
}
   
   
int lcm(int a,int b)
{
    int c=b;
   
    if(a<b)
    c=a,a=b,b=c; 
   
    b=a-b;
   
    if(b!=0)
    {   
     while(a%b!=0)
     {
      c=b;
      b=a%b;
      a=c;
     }
    }
    else
    b=c;
   
    return b;
   
}
int gcd(int c,int d,int e)
{
    e = c * d / e;
         
    return e;
   
}

巴斯卡三角形
Pascal's Triangle

[ 演算程式  ]
[  Pascal's Triangle Computer ( English Version )  ]

0 1 0 0 0 0
0 1 1 0 0 0
0 1 2 1 0 0
0 1 3 3 1 0
0 1 4 6 4 1
計算原理：如上面文字所列
每一格的數值即是( x , y )  ，其中 y 是由上往下數
套入公式  ( x , y ) = ( x-1 , y -1 ) + ( x , y-1 )        
使用陣列，馬上就能寫出來
Every number existed in the triangle can be expressed like ( x , y ) = ( x - 1 , y -1 ) + ( x , y - 1 )
Please notice that the " y " here , is counted from up to down.
( For example : ( 2 , 1 ) = 0      ( 2 , 2 ) = 1      ( 3 , 3 ) = 3  )
You can try to write a script to compute this triangle using the formula above. ( It's recommended to use array. )
在數學上的應用：
Usage of Pascal's Triangle in Mathematics

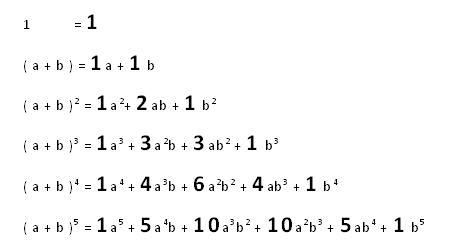原始碼 (使用最省記憶、最有效率的寫法)
#include<stdio.h>
#include<stdlib.h>
int  main ()
{
     int phase[34][2],counter,x,row,y;
       
    printf("  《楊輝三角形產生器》\n\n本程式可以輸出你輸入的列數\n\n任何時候都可以輸入-1離開\n\n(３２位元電腦只支援到34行)\n\n ");
   
    while(x==x)/* 無限迴圈開始 */
    {         
     for(x=0;x<=34;x++) /* 清空變數 */
    {
      for(y=0;y<=1;y++)
        phase[x][y]=0;
    }
       
     printf("請輸入顯示列數 : ");
     scanf("%d",&counter);
    
     printf("\n");
     if(counter>=35)
       counter=34;
     if(counter==-1) /* 使用者輸入 -1 離開 */
        break;
             
     phase[0][0]=1; /* 初始化計算用數值 */
    
     row=1;
    
       while(row<=counter) /* 程式跑到指定列數才結束 */
       {                                     
           for(x=1;x<=counter-row;x++) /* 美化用的迴圈... */
            printf(" ");
        for(x=1;x<=row;x++) /* 計算並顯示數值 */
        {
            phase[x][1]=phase[x-1][0]+phase[x][0];
            printf(" %d",phase[x][1]);
      
        }
       
          for(x=0;x<=row;x++) /* 放入這個迴圈的數值 讓下個迴圈計算 */
            phase[x][0]=phase[x][1];
      
       row++; /* 跑的列數 +1 */
    
       printf("\n\n");   
       }
     } /* 無限迴圈結束 */
     printf("(c) NTPU CSIE 49571602\n\n");
    
     system("pause");
    
     return 0;
} 
Pascal's Triangle Code. ( White Texts Hidden Below, for your reference. )
(Using the most efficient method, which saves most memory that I've ever tried.)
#include<stdio.h>
#include<stdlib.h>
int  main ()
{
     int phase[34][2],counter,x,row,y;
       
    printf("  << Pascal's Triangle Computer >>\n\nThis program computes the number of line you requested.\n\nYou may exit any time by typing -1\n\n( A 32-bit computer is limited to display less than 34 lines. )\n\n ");
   
    while(x==x)
    {         
     for(x=0;x<=34;x++)
    {
      for(y=0;y<=1;y++)
        phase[x][y]=0;
    }
       
     printf("For How many Lines would you like to Compute : ");
     scanf("%d",&counter);
    
     printf("\n");
     if(counter>=35)
       counter=34;
     if(counter==-1)
        break;
             
     phase[0][0]=1;
    
     row=1;
    
       while(row<=counter)
       {                                     
           for(x=1;x<=counter-row;x++)
            printf(" ");
        for(x=1;x<=row;x++) /* 計算並顯示數值 */
        {
            phase[x][1]=phase[x-1][0]+phase[x][0];
            printf(" %d",phase[x][1]);
      
        }
       
          for(x=0;x<=row;x++)
            phase[x][0]=phase[x][1];
      
       row++;
    
       printf("\n\n");   
       }
     }
     printf("(c) NTPU CSIE 49571602\n\n");
    
     system("pause");
    
     return 0;
}